Resolution

Resolution, 构造projective, injective, free和flat解消能够用来计算一系列导出函子. Resolution也是定义导出函子的前置. 这一节主要考虑projective resolution.

Resolution

We will consider chain complexes $A$ in $\mathrm{Ch}_{\geq 0}(\mathcal{A})$ .

A\qquad \cdots\xrightarrow{}A_{n}\xrightarrow{}A_{n-1}\xrightarrow{}\cdots \xrightarrow{}A_{0}\xrightarrow{}0

We first give definition to projective and acyclic complexes.

Definition 1. A chain complex $A$ is projective if $A_{n}$ is projective for $n\geq 0$ .

Definition 2. A chain complex $A$ is acyclic if $H_{n}(A)=0$ for all $n\geq 1$ .

The chain complex $A$ is acyclic if and only if the sequence

\cdots\xrightarrow{}A_{1}\xrightarrow{}A_{0}\xrightarrow{}H_{0}(A)\to 0

is exact.

Definition 3. An acyclic and projective complex is called a projective resolution of $H_{0}(A)$ .

The projective resolution of $A$ may not be the same, but they must be in the same homotopy type. We will prove this theorem.

Theorem 1. Let $A:\cdots\to A_{1}\to A_{0}\to 0$ and $B:\cdots \to B_{1}\to B_{0}\to 0$ be two chain complex. $A$ is projective and $B$ is acyclic. Then for every $\bar{f}:H_{0}(A)\to H_{0}(B)$ there exists a morphism $f:A\to B$ inducing $\bar{f}$ .

Proof

Proof. We construct the map $f:A\to B$ inductively.

First for $n=0$ :

Since the lower row is exact, by projectivity, $\exists f_{0}:A_{0}\to B_{0}$ with the diagram commutes.

Suppose for $n\geq 1$ , $f_{0},f_{1},dots,f_{n-1}$ are constructed. Consider the diagram

From the projectivity, we can find $f_{n}:A_{n}\to B_{n}$ with $f_{n-1}d_{n}=d_{n}f_{n}$ by considering the diagram:

Then we show the homotopy. Assume $f,g$ be two morphisms satisfying the condition. We define $h:f\to g$ inductively.

First for $n=0$ :

Since $f_{0}$ , $g_{0}$ both make the diagram commute, $f_{0}-g_{0}$ maps $A_{0}$ into
$\mathrm{Ker}(B_{0}\to H_{0}(B))=\mathrm{Im}(B_{1}\to B_{0})$ . From projectivity, $\exists h_{0}:A_{0}\to B_{1}$ with $f_{0}-g_{0}=d_{1}h_{0}$ by considering the diagram

Suppose for $n\geq 1$ we have $h_{0},\dots, h_{n-1}$ . Consider the diagram

\begin{aligned} d_{n}(f_{n}-g_{n}-h_{n-1}d_{n})&=f_{n-1}d_{n}-g_{n-1}d_{n}-d_{n}h_{n-1}d_{n}\\&=(f_{n-1}-g_{n-1}-d_{n}h_{n-1})d_{n}\\&=h_{n-2}d_{n-1}d_{n}=0\end{aligned}

From projectivity, we have $h_{n}:A_{n}\to B_{n+1}$ s.t. $f_{n}-g_{n}-h_{n-1}d_{n}=d_{n+1}h_{n}$ by considering the diagram

◻

Definition 4. We say abelian category $\mathcal{A}$ has enough projective if for every object $A$ , there is at least one projective object $P$ s.t. $P\xrightarrow{f}A\to 0$ exact. Then $0\to \mathrm{Ker}f\to P\xrightarrow{f}A\to 0$ is a short exact sequence.

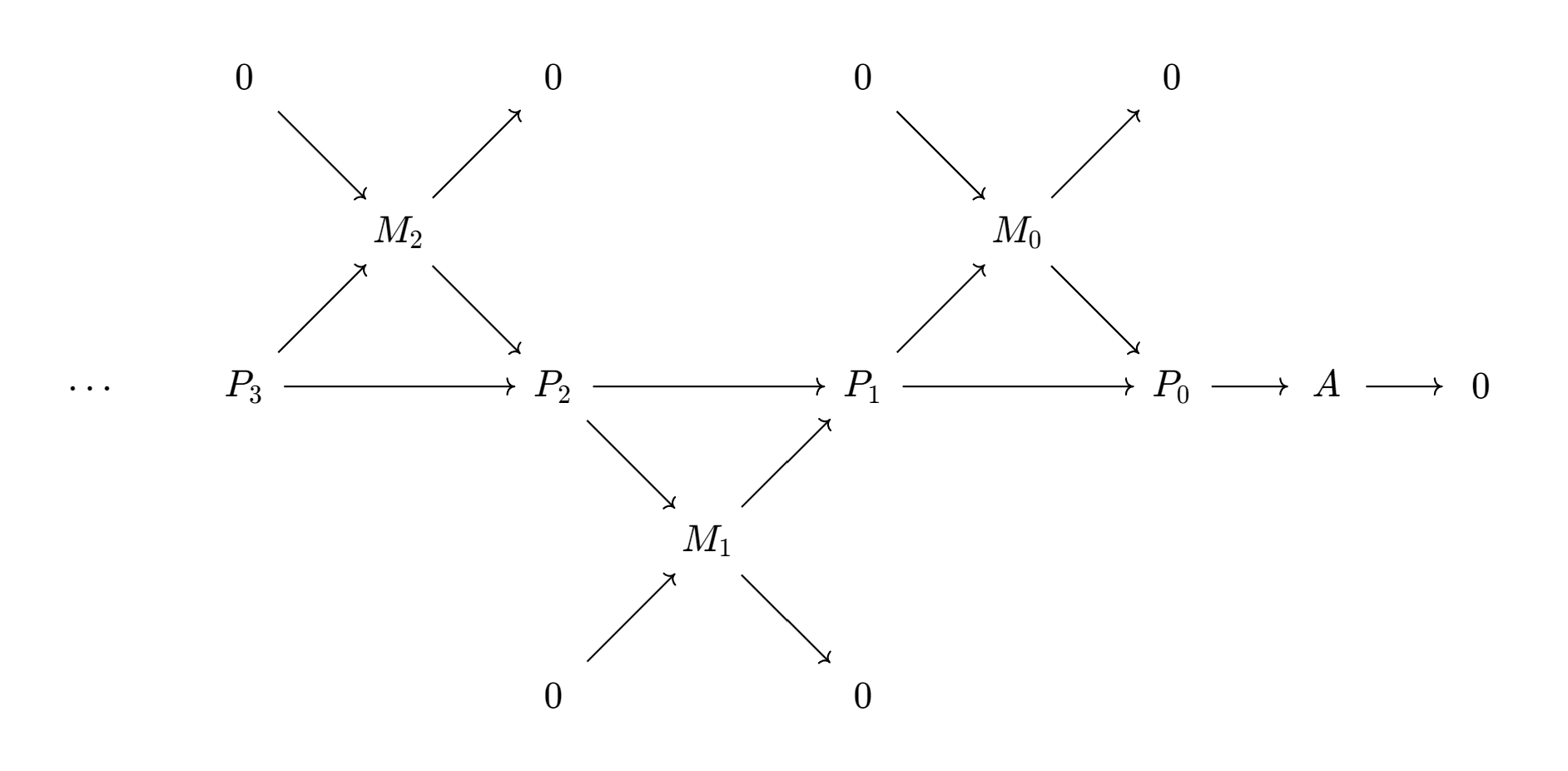
It’s not difficult to verify category $\mathrm{Mod}$ has enough projectives. We can construct a projective resolution for $A$ if category $\mathcal{A}$ has enough projectives. We can construct as the following diagram:

Theorem 2. Any two projective resolution of $A$ are the same homotopy type.

Proof

Proof. Obvious corollary of the preceeding theorem. ◻

For the injective resolution, it’s just the duality case of projectives resolution. We do not talk about it solely.